It’s been a long time coming but I’ve finally got round to making a website to house/collate resources for Core Maths. There are some great resources out there but they are somewhat spread out.
A key thing I’d like to work on is making a place for students to go to revise. I don’t think that really exists at the moment so I’m hoping that my website can be that place.
This blog isn’t going anywhere. I’ll still post here from time to time and will pick out the best bits to go on the site.
I take it you’d like to know the address?
Happy new year. Would you like some starter questions based around the face that it’s now 2024? Sorry if you came here thinking I had over 2000 starter questions for you!
Here’s an example:

I think they’ll be suitable for a range of ages and levels of maths difficulties. Please do let me know which ones went well.
Download the ppt here:
I’ve been looking for a long time for a comprehensive set of revision notes for the Core Maths course but couldn’t find something that did quite what I wanted. So, I’ve tried making my own.
I’m interested to hear what you think and then I can edit it a bit and build suggestions into any future ones I make.
It was with great delight that I was contacted to lead a session at the Mathematics Education Innovation (MEI) Conference this year. I’ve been to the conference before (write up here) and really enjoyed it so was pleased to be going again. A nice added bonus is that it was held at Keele university which is where I studied my Maths/Music joint honours degree and completed my PGCE.
I didn’t take as fully comprehensive notes as I should have but here are some brief thoughts on the sessions I went to.
Equity, Diversity and Inclusion at MEI – Sarah Denison and Nicole Cozens
I was looking forward to this session as one of my roles is as a sixth form tutor who oversees students going in to engineering and maths based courses. We often don’t have a great balance of female students saying they want to take engineering so I was keen to see what suggestions there were here.
One of the comments made during the presentation was that girls still lean towards ‘helping professions’ which was explained to mean ones that are overtly helpful to other people. Apparently, it isn’t clear that engineering/maths is ‘helpful’ (or certainly not so obviously as healthcare for example) so it was suggested that it’s worth coming at this from a Maths for Social Justice viewpoint to help dispel the myth that going into STEM is all about making money. I like that idea a lot and there is a padlet of resources available here.
More broadly, there was mention of the fact that our curriculum portrays the idea that maths was invented exclusively by white men from Northern Europe. Sarah has put together a padlet of resources aimed at diversifying the maths curriculum and we explored the fun activity Easy as 1, 2, 3…
Plenary session – Professor Emma McCoy
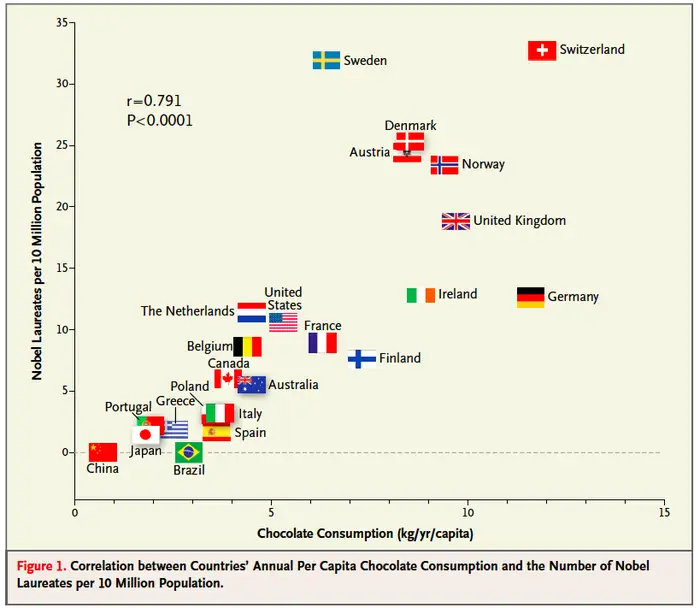
This was an engaging talk about the use of statistics and covered several practical examples of how it had been used to analyse situations such as whether Low Traffic Zones had improved air quality. There was mention of Simpson’s Paradox and some nice examples of Confidence Intervals in the wild with reference to reduction in road traffic accidents. Emma also mentioned the correlation between chocolate consumption (kg/yr/capita) and Nobel Laureates (per 10 million population). It was fun trying to decide what the confounding factors might be and I’m sure I’ll work this into a Core Maths resource soon.
Levelling up! – James Maloney
This talk was about the difference between GCSE questions and level three Core Maths questions. James had a quick quiz and then several examples for people to look at and discuss. Obviously this is something I am pretty familiar with but there are still some questions where it wasn’t obvious to me which specification it belongs to.
What was surprising to me was how many teachers simply didn’t know what Core Maths is. I can imagine that it’s hard to get the word out and, while think candidate numbers are still increasing, it’s still a relatively small qualification. I’m not quite sure what needs to be done about it but there’s still a long way to go with this qualification!
How can we recruit and retain the maths teachers needed to ensure our young people can access the maths education they need to thrive? – Charlie Stripp, John Westwell and Sharon Tripconey
This was a very topical talk with many of the participants speaking about how they are struggling to find maths teachers. Charlie said that MEI are in a position to speak to those in power about this and asked us what things we thought would help.
One interesting point that came up for me was the way the non-specialist teachers of maths are treated. They can be thought of as a last, desperate measure and, even if that is true, there’s no reason why they can’t be good teachers of maths. John suggested that we could help ourselves by telling other teachers about the positive aspects of being a maths teacher and actively encouraging others to try it.
Some of the ideas that were suggested by the group were:
- More pay
- Same pay but more non-contact time
- Timetable collaborative /observation planning time
- Head of Faculty being freed up from data/admin tasks to focus on improving the teaching of maths
- A move towards accepting that maths (and other) teachers are rarer and perhaps should be paid at different rates. Charlie mentioned that a well qualified maths teacher in Singapore could be on a similar pay point to the head teacher in recognition of their importance.
- Meaningful professional development for teachers that lead to qualifications (that lead to enhanced pay)
- Split the bursary to train so that some of it is paid if the person stays in teaching
It’s obvious that there’s no easy answer to this problem but I’m happier knowing that MEI might at least have some part to play in it.
Financial Maths – Making it Interesting – Me
My presentation was very well attended (thanks to everyone that came along) and had some lovely discussion about various financial topics. One of my main threads was that I think a good financial maths question is one where the fact that the context is money should be meaningful in some way. I gave examples of how compound interest questions could be reskinned into different contexts so I personally view them as being percentage questions more so than finance.
I looked at two questions and thought about ways we could improve one of them (see the file).
To finish, I gave some short starting ideas for financial maths questions. These mostly have a Core Maths feel to them but some are also designed to be applicable to younger students too.
Final Thoughts
I wasn’t able to stay for the second day but thoroughly enjoyed my time at the conference. It was great to see some thought provoking talks, visit the various trade stands and catch up with various mathsy folk that I’ve met across the years. If you get a chance to go to the next one, I’d thoroughly recommend it.
I’ve made a few more questions related to the Online Nation material. The graphs are from the original report so I’m not sharing the preliminary material itself.
It’s a little interesting to note that the charts have been changed slightly from the originals (link in the ppt). There’s a nice discussion to be had about which version is clearer.
Let me know what you think.
I thought you might be able to make use of these questions. Let me know what you think.
Question 1
Barry has 3 acres of land.
An acre is roughly 40 000 square feet.
How many trees can he plant on that land?
Question 2
I don’t mean to brag but I have a farm with about 1.1 million trees.
How big would you estimate my farm to be in acres?
(An acre is roughly 40 000 square feet.)
Question 3
It is expected that 8 million real Christmas trees will be bought next year.
There are plans to change the guidance on spacing so that trees should be 9 feet apart, rather than 8.
Under the new guidance, how much more space would 8 million trees need in acres?
Bonus finance question
Poppy took out a Student Loan in 2022.
She has an impressive salary of £99 997.30 per year.
Find out why she’s really satisfied by her annual loan repayment amount.
The Easter holidays are over and no doubt you’re beginning to focus on the imminent exams. Here are some Easter themed questions that you could use in your class as part of revision.

https://pixabay.com/images/id-7759286/
Paper 1 Questions
1) Cadbury’s Dairy Milk Freddo Faces Easter egg shrank this year from 122g to 96g but costing £1.25 instead of £1. What is the percentage change in pence per gram from last year to this year?
2) You want to carry out a survey of people in your school to find out how many easter eggs they ate over the holidays. Describe how you could use a random number generator to choose a sample.
3) A healthy eating campaign carries out a survey which includes the following question: “It seems like Easter eggs are on sale almost immediately after Christmas. Do you agree that seasonal products should be limited to how far in advance they can be on sale?” Melody thinks that this question is leading and trying to get people to agree with the campaign. What two aspects of the way the question is written make it leading?
4) I distrust the companies that make eggs and don’t believe they are selling me what I paid for. To test this, I weighed 10 eggs that were said to have a mass of 300g. The results were 299, 302, 302, 298, 298, 302, 299, 299, 299, 301. By finding the mean and standard deviation, of the eggs, does it seem likely that I have a valid cause for concern?
5) A survey asks 2083 people how many small easter eggs (like Cadbury Creme eggs) they had eaten this year. The table below shows the results:

a) Explain why it is difficult to find the mean number of eggs eaten
b) Assuming that the last category has a midpoint of 12, estimate the mean number of these sorts of eggs eaten per person
6) Estimate how many boxed easter eggs were sold in England this year.
Paper 2A Questions
7) When trying to predict the number of eggs to be delivered, it is suggested that the temperature may play a part. Over a number of years, the number of eggs delivered and temperature are found to have a PMCC of r=0.85. Interpret this value in context.
8) A particular type of egg is packaged with a mean weight of 205 grams and a standard deviation of 3g. The packaging claims a mass of 200 grams. Use the normal distribution to estimate what percentage of these eggs are underweight.
I’m afraid I don’t have time to put all the answers yet but here’s what I’ve got so far:
1) Last year was 0.8197 p/g and this year is 1.3021 p/g. The percentage change is about 59%
2) obtain a list of all the people in the school. Number them. Use a random number generator to select people until you have reached the desired sample size. Ignore repetitions or numbers that are above the number of people in the school.
3) The first sentence is unnecessary. It shouldn’t start, “Do you agree…”
4) Mean is 299.9 and sd is 1.6633. That’s very close to 300 and the sd is small. It’s inconclusive so a larger sample size would be a good idea.
5a) The group that’s 10 plus is difficult to deal with.
5b) Mean = 1.818 and sd = 3.196
6) I’ll let you figure this out!
7) This is a strong positive correlation. That means that in years when the temperature was higher, more eggs were delivered.
8) 4.7%
Last year, I made a basic list of things that I think very student should have an understanding of if they’re taking the Core Maths exams (AQA 2A). It was born out of a frustration with students approaching mock exams and clearly not knowing how to find the standard deviation for a set of data.
I always intended to make a more comprehensive list for students at the other end of the spectrum who wanted to be able to say that they had thoroughly revised/learnt everything they needed to. It’s taken a while but here it is, split into Paper 1 and Paper 2A:
Just in case you would like the fundamentals list, that’s here:
It’s every Core Maths teachers’ favourite time of year – preliminary material time. This year, I accidentally looked at the paper 1 material before guessing the context but my colleague, Lucy, spectacularly guessed “Something to do with trees?”! For paper 2, I guessed at something to do with cars or mobile phones so we’re feeling pretty good about our psychic abilities.
Anyway, you’re probably here for resources and, maybe, my thoughts on the material. I’m going to include links to other people’s thoughts too where possible. If you know of any I don’t, please do tell me so I can add them.
If you write a resource or question and would like me to share it here, then also please get in touch.
Thoughts
Paper 1 sees the much anticipated return of Income Tax and National Insurance. The format is pleasingly familiar and the numbers are what I was expecting. It’s a little unusual to have the 45% (additional) rate of tax included and this does make me wonder if they will give additional information about the personal allowance to work that into the question. The National Insurance is as expected and I must remember to actually do some monthly calculations with my students.
Student loans is a sensible financial focus. I’m going to talk about the change in tuition fee laws that explain why the threshold changed at September 2012. Other than that students don’t usually find this topic too bad as long as they just treat it as another ‘tax’ (ie it’s worked out on the gross salary). The mention of additional payments is interesting but my feeling is that that would vastly overcomplicate a question if that were used.
Christmas eh? I like this. A criticism of AQA I’ve had in the past is that the estimation question can be a little too easy to predict (the motorways and sweet factory felt like that) so it’s nice that this one is not completely obvious. I’m going to spend more time on this one later on but my intuition is something to do with “how much space would all of the Nordmann Firs that were sold in 2022 have needed to occupy while growing?” There are some other options (I think) but I’ll put them together another time.
The Paper 2 preliminary material is typically more difficult to enagage with and has more difficult questions. Having said that, I do think this year’s topic is interesting to students as they all use social media (critical analysis resource here) and the text is fairly accessible. I’ve made a fairly comprehensive familiarisation resource below and working through that gives you a fair sense of what I think about for each part. I’m sure I’ll write some more exam-style questions but essentially, I’m pretty happy with this material as being something to work with.
If you haven’t been to an AMSP meeting about this, I strongly recommend just showing students the graphs first, without labels/titles and asking them what they think about it before giving them all the text.
General Resources
My FAQ about what you can and can’t do with preliminary material is worth a read if you’re new to this.
As ever, Cat has put together a padlet with loads of useful links. They’re great for doing work around the preliminary materials and really digging in deep to the topics.
Resources for Paper 1
Here is a set of finance questions I made for the 2023 Preliminary material.
The finance resources for Tax, NI and Student Loans I’ve used this year are here.
I was asked in the comments about monthly National Insurance payments. Here’s a worksheet to take you through that.
Abby Beer has made an excellent Desmos Activity for students to practice their Tax and National Insurance work. Abby has also kindly let people have access to the editable teacher version.
Ellis Johnson has started to collate some possible questions along with a place for you to add your own ones.
Here’s something that Lucy and I have written about the trees.
Resources for Paper 2
I’ve made a familiarisation worksheet to help students read through the material. I was envisaging the classic Science text book with a double page spread and then questions that linked really clearly to each section.
As I’ve said above, if you have anything you’d like to share, get in touch and I’ll add it.
